Skaičių sistemos ir terminai

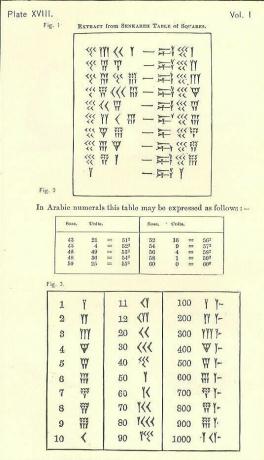
Trys pagrindinės sričių skirtumai nuo mūsų skaičių

Įsivaizduokite, kaip daug lengviau būtų išmokti aritmetikos ankstyvaisiais metais, jei viskas, ką jums reikėjo padaryti, būtų išmokti rašyti tokią liniją kaip aš ir trikampį. Iš esmės tai turėjo daryti visi senovės Mesopotamijos žmonės, nors jie įvairino čia ir ten, pailgindami, sukdami ir pan.

Jie neturėjo mūsų rašiklių ir pieštukų ar popieriaus tuo klausimu. Tai, ką jie parašė, buvo skulptūroje naudojamas įrankis, nes terpė buvo molio. Tai, ar tai išmokti sunkiau, ar lengviau, nei pieštuką, yra tikra mintis, tačiau kol kas jie yra lengvumo skyriuje ir turi tik du pagrindinius simbolius.

Kitas žingsnis mesti veržliaraktį į paprastumo skyrių. Mes naudojame a 10 bazė, sąvoka atrodo akivaizdi, nes turime 10 skaitmenų. Mes iš tikrųjų turime 20, bet tarkime, kad mes dėvime sandalus su apsauginėmis kojų dangomis, kad neatsiliktume nuo smėlio dykuma, karšta nuo tos pačios saulės, kuri keptų molio tabletes ir jas išsaugotų, kad rastume tūkstantmečius vėliau. Babiloniečiai naudojo šią bazę 10, bet tik iš dalies. Iš dalies jie naudojo „Base 60“ - tą patį skaičių, kurį matome aplinkui per minutes, sekundes ir trikampio ar apskritimo laipsnius. Jie buvo patyrę astronomai ir todėl skaičius galėjo kilti iš jų stebėjimų iš dangaus. „Base 60“ taip pat turi įvairių naudingų veiksnių, kuriuos naudojant lengva apskaičiuoti. Vis dėlto mokytis „Base 60“ baugina.

„Pagarba Babilonijai“ [Matematinis leidinys, Tomas 76, Nr. 475, „Matematikos istorijos panaudojimas mokant matematikos“ (1992 m. Kovo mėn.), P. 158–178], rašytojas-mokytojas Nickas Mackinnonas sako, kad naudoja babiloniečių matematiką mokydamas 13 metų amžiaus vaikus, išskyrus pagrindus. Babilono sistema naudoja bazę-60, tai reiškia, kad vietoj dešimtainio skaičiaus ji yra lygiavertė.

Tiek Babilonijos skaičių sistema, tiek mūsiškiai pasikliauja pozicija, kad suteiktų vertę. Abi sistemos tai daro skirtingai, iš dalies todėl, kad jų sistemai trūko nulio. Išmokti babiloniečių padėties kairėje į dešinę (nuo žemos iki žemos) pagal pirmąjį pagrindinio aritmetikos skonį tikriausiai ne daugiau sudėtinga, nei išmokti mūsų 2 krypčių, kur turime atsiminti dešimtainių skaičių tvarką - didinti nuo dešimtainės, tokių, dešimtys, šimtai, o paskui žvilgčioja kita kryptimi iš kitos pusės, nėra nė vienos ons kolonos, tik dešimtosios, šimtosios, tūkstantosios ir kt.

Aš gilinsiuosi į Babilono sistemos pozicijas kituose puslapiuose, bet pirmiausia reikia išmokti keletą svarbių skaičių žodžių.

Mes kalbame apie metų laikotarpius, naudodami dešimtainius dydžius. Mes turime dešimtmetį 10 metų, šimtmetį 100 metų (10 dešimtmečių) arba 10X10 = 10 metų kvadratu, o tūkstantmetį 1000 metų (10 šimtmečių) arba 10X100 = 10 metų kubeliais. Aš nežinau jokio aukštesnio termino, bet tai nėra tie vienetai, kuriuos naudojo babiloniečiai. Nickas Mackinnonas nurodo Senkareho (Larsa) iš sero Henrio Rawlinsono (1810–1895) * planšetinius kompiuterius, naudojamus vienetams, kuriuos naudojo babiloniečiai, ne tik už tuos metus, bet ir numatomus kiekius:

1. soss
2. nervas
3. sar.

sossnersosssarsoss

Vis dar nėra kaklaraiščio pertraukiklio: nebūtinai lengviau išmokti kvadratinių ir kubinių metų terminus iš lotynų kalbos tai yra vienbalsiai babiloniečių žodžiai, kuriuose nėra brūkšniavimas, o dauginimas iš 10.

Ką tu manai? Ar būtų buvę sunkiau išmokti skaičių pagrindų kaip babiloniečio mokyklos vaikui ar kaip šiuolaikiniam mokiniui angliškai kalbančioje mokykloje?

* George'as Rawlinsonas (1812–1902), Henriko brolis, rodo supaprastintą perrašytą kvadratų lentelę Septynios didžiosios senovės Rytų pasaulio monarchijos. Lentelė atrodo astronominė, pagrįsta Babilono metų kategorijomis.

Visos nuotraukos yra iš šio internetinio nuskaityto XIX a. Leidimo George Rawlinson's versijos Septynios didžiosios senovės Rytų pasaulio monarchijos.

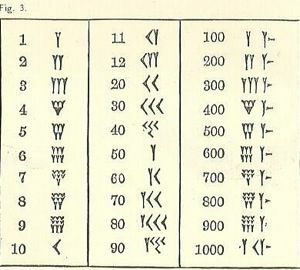
Kadangi mes užaugome su kita sistema, babiloniečių skaičiai yra painūs.

Bent skaičiai skaičiuojami nuo aukšto kairėje iki žemo dešinėje, kaip mūsų arabų sistemoje, bet likusieji tikriausiai atrodys nepažįstami. Vieno simbolis yra pleišto arba Y formos. Deja, Y taip pat reiškia 50. Yra keletas atskirų simbolių (visi pagrįsti pleištu ir linija), tačiau visi kiti skaičiai yra suformuoti iš jų.

Atminkite, kad rašymo forma yra cuneiform arba pleišto formos. Dėl įrankio, naudojamo brėžti linijas, jo pasirinkimas yra ribotas. Pleištas gali turėti arba neturėti uodegos, nubrėžtos cuneiformos rašymo plunksna išilgai molio, įspaudus dalį trikampio formos.

10, apibūdinamų kaip strėlės galvutė, atrodo šiek tiek kaip

Trys iki 3 mažų 1 eilutės (parašytos kaip Y su šiek tiek sutrumpintomis uodegomis) arba 10 (10 parašytos taip, kaip

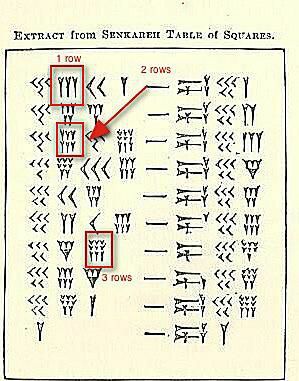
Yra trys cuneiform skaičių rinkiniai klasteriai paryškinta aukščiau esančioje iliustracijoje.

Šiuo metu mes nesirūpiname jų verte, o norime parodyti, kaip galėtumėte pamatyti (arba parašyti) bet kurioje vietoje nuo 4 iki 9 to paties skaičiaus, sugrupuoto. Trys eina iš eilės. Jei yra ketvirtas, penktas ar šeštas, jis eina žemiau. Jei yra septintas, aštuntas ar devintas, jums reikia trečios eilutės.

Tolesniuose puslapiuose pateikiamos instrukcijos, kaip atlikti skaičiavimus su babiloniečių kasykla.

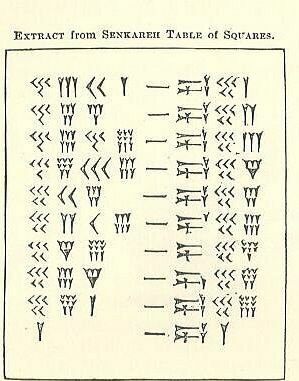
Iš to, ką jūs skaitėte aukščiau apie soss - kurį atsiminsite 60 metų Babilonietis, pleištas ir strėlės galvutė - kurie yra aprašomieji cuneiform ženklų pavadinimai, pažiūrėkite, ar galite suprasti, kaip šie skaičiavimai veikia. Viena brūkšnį primenančio ženklo pusė yra skaičius, o kita - kvadratas. Išbandykite kaip grupę. Jei negalite išsiaiškinti, pažiūrėkite į kitą žingsnį.

Ar galite tai išsiaiškinti dabar? Duok šansą.

...

Kairėje pusėje yra 4 aiškūs stulpeliai, po jais brūkšnys panašus ženklas ir 3 stulpeliai dešinėje. Žiūrint iš kairės pusės, 1s stulpelio ekvivalentas iš tikrųjų yra 2 stulpeliai, arčiausiai „brūkšnio“ (vidiniai stulpeliai). Kiti 2 išoriniai stulpeliai skaičiuojami kartu kaip 60-asis stulpelis.

• 4
• 3-Y = 3.
• 40+3=43.
• Vienintelė problema yra ta, kad po jų yra kitas numeris. Tai reiškia, kad jie nėra vienetai (jų vieta). 43 yra ne 43, bet 43–60, nes tai yra seksualesnioji (bazinė-60) sistema ir yra soss stulpelį, kaip rodo apatinė lentelė.
• Padauginkite 43 iš 60, kad gautumėte 2580.
• Pridėti kitą numerį (2
• Dabar jūs turite 2601.
• Štai 51 kvadratas.

Kitoje eilutėje yra 45 taškai soss stulpelį, taigi jūs padauginsite 45 iš 60 (arba 2700), o tada pridėkite 4 iš stulpelio vienetų, taigi turite 2704. 2704 kvadratinė šaknis yra 52.

Ar galite suprasti, kodėl paskutinis skaičius = 3600 (60 kvadratų)? Užuomina: Kodėl ne 3000?